Prêts, feu, partez !

Bien, démarrons ! Si vous êtes le genre de personne horrible qui ne lit pas les introductions et que vous l’ayez sautée, vous feriez peut-être bien de tout de même lire la dernière section de l’introduction, car elle explique ce dont vous avez besoin pour suivre ce tutoriel et comment l’on va charger des fonctions. La première chose qu’on va faire, c’est lancer un GHC interactif et appeler quelques fonctions pour se faire une première idée de Haskell. Ouvrez donc votre terminal et tapez ghci. Vous serez accueilli par un message semblable à celui-ci.

GHCi, version 6.8.2: http://www.haskell.org/ghc/  :? for help
Loading package base ... linking ... done.
Prelude>

Bravo, vous êtes dans GHCi ! L’invite Prelude> peut devenir de plus en plus longue lorsqu’on importera des choses dans la session, alors on va la remplacer par ghci>. Si vous voulez la même invite, tapez simplement :set prompt "ghci> ".

Voici un peu d’arithmétique élémentaire.

ghci> 2 + 15
17
ghci> 49 * 100
4900
ghci> 1892 - 1472
420
ghci> 5 / 2
2.5
ghci>

C’est plutôt simple. Nous pouvons également utiliser plusieurs opérateurs sur la même ligne, et les règles de précédence habituelles s’appliquent alors. On peut également utiliser des parenthèses pour rendre la précédence explicite, ou l’altérer.

ghci> (50 * 100) - 4999
1
ghci> 50 * 100 - 4999
1
ghci> 50 * (100 - 4999)
-244950

Plutôt cool, non ? Ouais, je sais que c’est pas terrible, mais supportez-moi encore un peu. Attention, un écueil à éviter ici est la négation des nombres. Pour obtenir un nombre négatif, il est toujours mieux de l’entourer de parenthèses. Faire 5 * -3 vous causera les fureurs de GHCi, alors que 5 * (-3) fonctionnera sans souci.

L’algèbre booléenne est également simple. Comme vous le savez sûrement, && représente un et booléen, || un ou booléen, et not retourne la négation de True et False (NdT: respectivement vrai et faux).

ghci> True && False
False
ghci> True && True
True
ghci> False || True
True
ghci> not False
True
ghci> not (True && True)
False

Un test d’égalité s’écrit ainsi :

ghci> 5 == 5
True
ghci> 1 == 0
False
ghci> 5 /= 5
False
ghci> 5 /= 4
True
ghci> "hello" == "hello"
True

Et que se passe-t-il si l’on fait 5 + "llama" ou 5 == True ? Eh bien, si on essaie le premier, on obtient un gros message d’erreur effrayant !

No instance for (Num [Char])
    arising from a use of `+' at <interactive>:1:0-9
    Possible fix: add an instance declaration for (Num [Char])
    In the expression: 5 + "llama"
    In the definition of `it': it = 5 + "llama"

Beurk ! Ce que GHCi essaie de nous dire, c’est que "llama" n’est pas un nombre, et donc qu’il ne sait pas l’additionner à 5. Même si ce n’était pas "llama" mais "four" ou même "4", Haskell ne considérerait pas cela comme un nombre. + attend comme opérandes à droite et à gauche des nombres. Si on essayait de faire True == 5, GHCi nous dirait que les types ne correspondent pas. Ainsi, + ne fonctionne qu’avec des paramètres pouvant être considérés comme des nombres, alors que == marche sur n’importe quelles deux choses à condition qu’on puisse les comparer. Le piège, c’est qu’elles doivent être toutes les deux du même type de choses. On ne compare pas des pommes et des oranges. Nous nous intéresserons de plus près aux types plus tard. Notez : vous pouvez tout de même faire 5 + 4.0 car 5 est vicieux et peut se faire passer pour un entier ou pour un nombre à virgule flottante. 4.0 ne peut pas se faire passer pour un entier, donc c’est à 5 de s’adapter à lui.

Vous ne le savez peut-être pas, mais nous venons d’utiliser des fonctions tout du long. Par exemple, * est une fonction qui prend deux nombres et les multiplie entre eux. Comme vous l’avez constaté, on l’appelle en le mettant en sandwich entre ces paramètres. C’est pour ça qu’on dit que c’est une fonction infixe. La plupart des fonctions qu’on n’utilise pas avec des nombres sont des fonctions préfixes. Intéressons-nous à celles-ci.

Les fonctions sont généralement préfixes, donc à partir de maintenant, nous ne préciserons pas qu’une fonction est préfixe, on le supposera par défaut. Dans la plupart des langages impératifs, les fonctions sont appelées en écrivant le nom de la fonction, puis ses paramètres entre parenthèses, généralement séparés par des virgules. En Haskell, les fonctions sont appelées en écrivant le nom de la fonction, puis une espace, puis ses paramètres, séparés par des espaces. Par exemple, essayons d’appeler une des fonctions les plus ennuyantes d’Haskell.

ghci> succ 8
9

La fonction succ prend n’importe quoi qui a un successeur, et renvoie ce successeur. Comme vous pouvez le voir, on sépare le nom de la fonction du paramètre par une espace. Appeler une fonction avec plusieurs paramètres est aussi simple. Les fonctions min et max prennent deux choses qu’on peut ordonner (comme des nombres !). min retourne la plus petite, max la plus grande. Voyez vous-même :

ghci> min 9 10
9
ghci> min 3.4 3.2
3.2
ghci> max 100 101
101

L’application de fonction (appeler une fonction en mettant une espace après puis ses paramètres) a la plus grande des précédences. Cela signifie pour nous que les deux déclarations suivantes sont équivalentes.

ghci> succ 9 + max 5 4 + 1
16
ghci> (succ 9) + (max 5 4) + 1
16

Cependant, si nous voulions obtenir le successeur du produit des nombres 9 et 10, on ne pourrait pas écrire succ 9 * 10, car cela chercherait le successeur de 9, et le multiplierait par 10. Donc 100. Nous devrions écrire succ (9 * 10) pour obtenir 91.

Si une fonction prend deux paramètres, on peut aussi l’appeler de façon infixe en l’entourant d’apostrophes renversées. Par exemple, la fonction div prend deux entiers et effectue leur division entière. Faire div 92 10 retourne 9. Mais quand on l’appelle de cette façon, on peut se demander quel nombre est divisé par quel nombre. On peut donc l’écrire plutôt 92 `div` 10, ce qui est tout de suite plus clair.

Beaucoup de personnes venant de langages impératifs ont pour habitude de penser que les parenthèses indiquent l’application de fonctions. Par exemple, en C, on utilise des parenthèses pour appeler des fonctions comme foo(), bar(1) ou baz(3, "haha"). Comme nous l’avons vu, les espaces sont utilisés pour l’application de fonctions en Haskell. Donc, en Haskell, on écrirait foo, bar 1 et baz 3 "haha". Si vous voyez quelque chose comme bar (bar 3), cela ne veut donc pas dire que bar est appelé avec les paramètres bar et 3. Cela signifie qu’on appelle la fonction bar avec un paramètre 3 pour obtenir un nombre, et qu’on appelle bar à nouveau sur ce nombre. En C, cela serait bar(bar(3)).

Nos premières fonctions

Dans la section précédente, nous avons eu un premier aperçu de l’appel de fonctions. Essayons maintenant de créer les nôtres ! Ouvrez votre éditeur de texte favori et entrez cette fonction qui prend un nombre et le multiplie par deux.

doubleMe x = x + x

Les fonctions sont définies de la même façon qu’elles sont appelées. Le nom de la fonction est suivi de ses paramètres, séparés par des espaces. Mais lors de la définition d’une fonction, un = suivi de la définition de ce que la fonction fait suivent. Sauvez ceci en tant que baby.hs ou quoi que ce soit. À présent, naviguez jusqu’à l’endroit où vous l’avez sauvegardé, et lancez ghci d’ici. Une fois lancé, tapez :l baby. Maintenant que notre script est chargé, on peut jouer avec la fonction que l’on vient de définir.

ghci> :l baby
[1 of 1] Compiling Main             ( baby.hs, interpreted )
Ok, modules loaded: Main.
ghci> doubleMe 9
18
ghci> doubleMe 8.3
16.6

Puisque + fonctionne sur des entiers aussi bien que sur des nombres à virgule flottante (tout ce que l’on peut considérer comme un nombre en fait), notre fonction fonctionne également sur n’importe quel nombre. Créons une fonction prenant deux nombres et les multipliant chacun par deux, puis les sommant ensemble.

doubleUs x y = x*2 + y*2

Simple. Nous aurions également pu l’écrire doubleUs x y = x + x + y + y. Un test produit les résultats attendus (rappelez-vous bien d’ajouter cette fonction à la fin de baby.hs, de sauvegarder le fichier, et de faire :l baby dans GHCi).

ghci> doubleUs 4 9
26
ghci> doubleUs 2.3 34.2
73.0
ghci> doubleUs 28 88 + doubleMe 123
478

Comme attendu, vous pouvez appeler vos propres fonctions depuis les autres fonctions que vous aviez créées. Avec cela en tête, redéfinissons doubleUs ainsi :

doubleUs x y = doubleMe x + doubleMe y

Ceci est un exemple simple d’un motif récurrent en Haskell. Créer des fonctions basiques, qui sont visiblement correctes, puis les combiner pour faire des fonctions plus complexes. De cette manière, on évite la répétition. Que se passerait-il si un mathématicien se rendait compte que 2 est en fait 3 et qu’il fallait changer votre programme ? Vous pourriez simplement rédéfinir doubleMe comme x + x + x et, puisque doubleUs appelle doubleMe, elle fonctionnerait automatiquement dans cet étrange nouveau monde où 2 est 3.

Les fonctions en Haskell n’ont pas à être dans un ordre particulier, donc il n’importe pas que vous définissiez doubleMe puis doubleUs ou l’inverse.

Maintenant, nous allons écrire une fonction qui multiplie un nombre par 2, mais seulement si ce nombre est inférieur ou égal à 100, parce que les nombres supérieurs à 100 sont déjà bien assez gros comme ça !

doubleSmallNumber x = if x > 100
                        then x
                        else x*2

Ici, nous avons introduit la construction if de Haskell. Vous êtes probablement habitué aux constructions if des autres langages. La différence entre le if de Haskell et celui des autres langages, c’est qu’en Haskell, le else est obligatoire. Dans les langages impératifs, vous pouvez sauter quelques étapes si la condition n’est pas satisfaite, mais en Haskell, chaque expression doit renvoyer quelque chose. Nous aurions aussi pu écrire ce if en une ligne mais je trouve cette version plus lisible. Un autre point à noter est que la construction if en Haskell est une expression. Une expression correspond simplement à tout bout de code retournant une valeur. 5 est une expression car elle retourne 5, 4 + 8 est une expression, x + y est une expression car elle retourne la somme de x et y. Puisque le else est obligatoire, une construction if retournera toujours quelque chose, c’est pourquoi c’est une expression. Si nous voulions ajouter 1 à chaque nombre produit dans la fonction précédente, nous aurions pu l’écrire ainsi.

doubleSmallNumber' x = (if x > 100 then x else x*2) + 1

Si nous avions omis les parenthèses, nous aurions ajouté 1 seulement si x était plus petit que 100. Remarquez le ' à la fin du nom de la fonction. Cette apostrophe n’a pas de signification spéciale en Haskell. C’est un caractère valide à utiliser dans un nom de fonction. On utilise habituellement ' pour indiquer la version stricte d’une fonction (une version qui n’est pas paresseuse) ou pour la version légèrement modifiée d’une fonction ou d’une variable. Puisque ' est un caractère valide dans le nom d’une fonction, on peut écrire :

conanO'Brien = "It's a-me, Conan O'Brien!"

Il y a deux choses à noter ici. La première, c’est que dans le nom de la fonction, nous n’avons pas mis de majuscule au prénom de Conan. C’est parce que les fonctions ne peuvent pas commencer par une majuscule. Nous verrons pourquoi un peu plus tard. La seconde chose, c’est que la fonction ne prend aucun paramètre. Lorsqu’une fonction ne prend pas de paramètre, on dit généralement que c’est une définition (ou un nom). Puisqu’on ne peut pas changer ce que les noms (et les fonctions) signifient une fois qu’on les a définis, conanO'Brien et la chaîne "It's a-me, Conan O'Brien!" peuvent être utilisés de manière interchangeable.

Introduction aux listes

Tout comme les listes de courses dans le monde réel, les listes Haskell sont très utiles. C’est la structure de données la plus utilisée, et elle peut l’être d’une multitude de façons pour modéliser et résoudre tout un tas de problèmes. Les listes sont TROP géniales. Dans cette section, nous allons découvrir les bases des listes, des chaînes de caractères (qui sont en fait des listes) et des listes en compréhension.

En Haskell, les listes sont des structures de données homogènes. Elles contiennent plusieurs éléments du même type. Cela signifie qu’on peut avoir une liste d’entiers, une liste de caractères, mais jamais une liste qui a à la fois des entiers et des caractères. Place à une liste !

ghci> let lostNumbers = [4,8,15,16,23,42]
ghci> lostNumbers
[4,8,15,16,23,42]

Comme vous pouvez le constater, les listes sont dénotées par des crochets, et les valeurs d’une liste sont séparées par des virgules. Si on essayait une liste comme [1, 2, 'a', 3, 'b', 'c', 4], Haskell se plaindrait que des caractères (qui, d’ailleurs, sont dénotés comme un caractère entouré d’apostrophes) ne sont pas des nombres. En parlant de caractères, les chaînes de caractères sont simplement des listes de caractères. "hello" est simplement du sucre syntaxique pour ['h', 'e', 'l', 'l', 'o']. Puisque les chaînes de caractères sont des listes, on peut utiliser les fonctions de listes sur celles-ci, ce qui s’avère très pratique.

Une tâche courante consiste à coller deux listes l’une à l’autre. Ceci est réalisé à l’aide de l’opérateur ++.

ghci> [1,2,3,4] ++ [9,10,11,12]
[1,2,3,4,9,10,11,12]
ghci> "hello" ++ " " ++ "world"
"hello world"
ghci> ['w','o'] ++ ['o','t']
"woot"

Attention lors de l’utilisation répétée de l’opérateur ++ sur de longues chaînes. Lorsque vous accolez deux listes (et même si vous accolez une liste singleton à une autre liste, par exemple : [1, 2, 3] ++ [4]), en interne, Haskell doit parcourir la liste de gauche en entier. Ceci ne pose pas de problème tant que les listes restent de taille raisonnable. Mais accoler une liste à la fin d’une liste qui contient cinquante millions d’éléments risque de prendre du temps. Cependant, placer quelque chose au début d’une liste en utilisant l’opérateur : (aussi appelé l’opérateur cons) est instantané.

ghci> 'A':" SMALL CAT"
"A SMALL CAT"
ghci> 5:[1,2,3,4,5]
[5,1,2,3,4,5]

Remarquez comme : prend un nombre et une liste de nombres, ou bien un caractère et une liste de caractères, alors que ++ prend deux listes. Même si vous voulez ajouter un seul élément à la fin d’une liste avec ++, vous devez l’entourer de crochets pour en faire d’abord une liste.

[1, 2, 3] est en fait du sucre syntaxique pour 1:2:3:[]. [] est la liste vide. Si nous ajoutons 3 devant elle, elle devient [3]. Si nous ajoutons encore 2 devant, elle devient [2, 3], etc.

Si vous voulez obtenir un élément d’une liste par son index, utilisez !!. Les indices démarrent à 0.

ghci> "Steve Buscemi" !! 6
'B'
ghci> [9.4,33.2,96.2,11.2,23.25] !! 1
33.2

Mais si vous essayez d’obtenir le sixième élément d’une liste qui n’en a que quatre, vous obtiendrez une erreur, soyez donc vigilant !

Les listes peuvent aussi contenir des listes. Elles peuvent même contenir des listes qui contiennent des listes…

ghci> let b = [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b ++ [[1,1,1,1]]
[[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3],[1,1,1,1]]
ghci> [6,6,6]:b
[[6,6,6],[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]]
ghci> b !! 2
[1,2,2,3,4]

Plusieurs listes à l’intérieur d’une liste peuvent avoir des longueurs différentes, mais elles ne peuvent pas être de types différents. Tout comme l’on ne peut pas avoir une liste contenant quelques caractères et quelques nombres, on ne peut pas avoir de liste qui contient quelques listes de caractères et quelques listes de nombres.

Les listes peuvent être comparées si ce qu’elles contiennent peut être comparé. En utilisant <, <=, > et >= pour comparer des listes, celles-ci sont comparées par ordre lexicographique. D’abord, les têtes sont comparées. Si elles sont égales, alors les éléments en deuxième position sont comparés, etc.

ghci> [3,2,1] > [2,1,0]
True
ghci> [3,2,1] > [2,10,100]
True
ghci> [3,4,2] > [3,4]
True
ghci> [3,4,2] > [2,4]
True
ghci> [3,4,2] == [3,4,2]
True

Que peut-on faire d’autre avec des listes ? Voici quelques fonctions de base qui opèrent sur des listes.

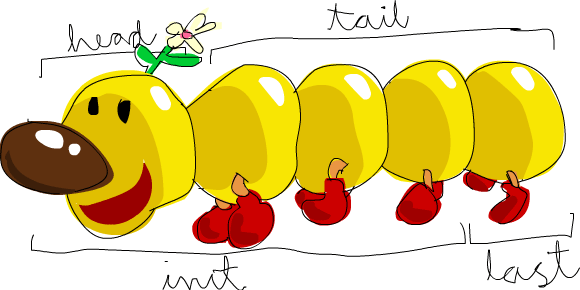
head prend une liste et retourne sa tête. La tête est simplement le premier élément.

ghci> head [5,4,3,2,1]
5

tail prend une liste et retourne sa queue. En d’autres termes, elle coupe la tête de la liste.

ghci> tail [5,4,3,2,1]
[4,3,2,1]

last prend une liste et retourne son dernier élément.

ghci> last [5,4,3,2,1]
1

init prend une liste et retourne tout sauf son dernier élément.

ghci> init [5,4,3,2,1]
[5,4,3,2]

En imaginant une liste comme un monstre, voilà ce que ça donne.

Mais que se passe-t-il si l’on essaie de prendre la tête d’une liste vide ?

ghci> head []
*** Exception: Prelude.head: empty list

Mon dieu ! Tout nous pète à la figure ! S’il n’y a pas de monstre, il ne peut pas avoir de tête. Lors de l’utilisation de head, tail, last et init, faites attention à ne pas les utiliser sur des listes vides. Cette erreur ne peut pas être détectée à la compilation, donc il est toujours de bonne pratique de prendre ses précautions pour ne pas demander à Haskell des éléments d’une liste vide.

length prend une liste et retourne sa longueur.

ghci> length [5,4,3,2,1]
5

null teste si une liste est vide. Si c’est le cas, elle retourne True, sinon False. Utilisez cette fonction plutôt que d’écrire xs == [] (si votre liste s’appelle xs).

ghci> null [1,2,3]
False
ghci> null []
True

reverse renverse une liste.

ghci> reverse [5,4,3,2,1]
[1,2,3,4,5]

take prend un nombre et une liste. Elle extrait ce nombre d’éléments du début de la liste. Regardez.

ghci> take 3 [5,4,3,2,1]
[5,4,3]
ghci> take 1 [3,9,3]
[3]
ghci> take 5 [1,2]
[1,2]
ghci> take 0 [6,6,6]
[]

Voyez comme, si l’on essaie de prendre plus d’éléments que la liste n’en contient, elle retourne la liste entière. Si on essaie d’en prendre 0, on obtient une liste vide.

drop marche d’une manière similaire, mais elle jette le nombre d’éléments demandé du début de la liste.

ghci> drop 3 [8,4,2,1,5,6]
[1,5,6]
ghci> drop 0 [1,2,3,4]
[1,2,3,4]
ghci> drop 100 [1,2,3,4]
[]

maximum prend une liste de choses qui peuvent être ordonnées et retourne la plus grande d’entre elles.

minimum retourne la plus petite.

ghci> minimum [8,4,2,1,5,6]
1
ghci> maximum [1,9,2,3,4]
9

sum prend une liste de nombres et retourne leur somme.

product prend une liste de nombres et retourne leur produit.

ghci> sum [5,2,1,6,3,2,5,7]
31
ghci> product [6,2,1,2]
24
ghci> product [1,2,5,6,7,9,2,0]
0

elem prend une chose et une liste de choses, et nous indique si cette première apparaît dans la liste. On l’utilise généralement de manière infixe car c’est plus simple à lire.

ghci> 4 `elem` [3,4,5,6]
True
ghci> 10 `elem` [3,4,5,6]
False

C’était un premier tour des fonctions qui opèrent sur des listes. Nous en verrons d’autres plus tard.

Texas rangées

Que faire si l’on veut la liste des nombres de 1 à 20 ? Bien sûr, on pourrait les taper un par un, mais ce n’est pas une solution pour des gentlemen qui demandent l’excellence de leurs langages de programmation. Nous utiliserons plutôt des progressions (NDT : qui sont appelées “ranges” en anglais, d’où le titre de cette section). Les progressions sont un moyen de créer des listes qui sont des suites arithmétiques d’éléments qui peuvent être énumérés. Les nombres peuvent être énumérés. Un, deux, trois, quatre, etc. Les caractères peuvent aussi être énumérés. L’alphabet est une énumération des caractères de A à Z. Les noms ne peuvent pas être énumérés. Qu’est-ce qui suit “John” ? Je ne sais pas.

Pour créer une liste contenant tous les entiers naturels de 1 à 20, on écrit [1..20]. C’est équivalent à [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20], et il n’y a aucune différence si ce n’est qu’écrire la séquence manuellement est stupide.

ghci> [1..20]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
ghci> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
ghci> ['K'..'Z']
"KLMNOPQRSTUVWXYZ"

Les progressions sont cool car on peut préciser un pas. Que faire si l’on cherche les nombres pairs entre 1 et 20 ? Ou un nombre sur trois ?

ghci> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
ghci> [3,6..20]
[3,6,9,12,15,18]

Il suffit juste de séparer les deux premiers éléments par une virgule, puis de spécifier la borne supérieure. Bien que plutôt intelligentes, les progressions ne sont pas aussi intelligentes que ce que certaines personnes attendent. Vous ne pouvez pas écrire [1, 2, 4, 8, 16..100] en espérant obtenir les puissances de 2. Premièrement, parce qu’on ne peut spécifier qu’un pas. Secondement, parce que certaines progressions non arithmétiques sont ambigües lorsqu’on ne les énonce que par leurs premiers éléments.

Pour créer une liste des nombres de 20 à 1, vous ne pouvez pas écrire [20..1], vous devez écrire [20, 19..1].

Attention lors de l’utilisation de nombres à virgule flottante dans les progressions ! N’étant pas entièrement précis (par définition), leur utilisation peut donner des résultats originaux.

ghci> [0.1, 0.3 .. 1]
[0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]

Mon avis est de ne pas les utiliser dans les progressions.

Vous pouvez aussi utiliser les progressions pour définir des listes infinies, simplement en ne précisant pas de borne supérieure. Nous verrons les détails des listes infinies un peu plus tard. Pour l’instant, examinons comment l’on pourrait obtenir les 24 premiers multiples de 13. Bien sûr, vous pourriez écrire [13, 26..24*13]. Mais il y a une meilleure façon de faire : take 24 [13, 26..]. Puisqu’Haskell est paresseux, il ne va pas essayer d’évaluer la liste infinie immédiatement et ne jamais terminer. Il va plutôt attendre de voir ce que vous voulez obtenir de cette liste infinie. Ici, il voit que vous ne voulez que les 24 premiers éléments, et il s’exécute poliment.

Une poignée de fonctions produit des listes infinies :

cycle prend une liste et la cycle en une liste infinie. Si vous essayiez d’afficher le résultat, cela continuerait à jamais, donc il faut la couper quelque part.

ghci> take 10 (cycle [1,2,3])
[1,2,3,1,2,3,1,2,3,1]
ghci> take 12 (cycle "LOL ")
"LOL LOL LOL "

repeat prend un élément et produit une liste infinie contenant uniquement cet élément. Cela correspond à cycler une liste à un élément.

ghci> take 10 (repeat 5)
[5,5,5,5,5,5,5,5,5,5]

Cependant, il est plus simple d’utiliser la fonction replicate pour obtenir un certain nombre de fois le même élément dans une liste. replicate 3 10 retourne [10, 10, 10].

Je suis une liste en compréhension

Si vous avez déjà suivi une classe de mathématiques, vous avez probablement déjà rencontré des ensembles définis en compréhension. On les utilise généralement pour construire des ensembles plus spécifiques à partir d’autres ensembles plus généraux. Une compréhension simple d’un ensemble qui contient les dix premiers entiers naturels pairs est 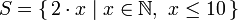. La partie située devant la barre verticale est la fonction qui produit la sortie, x est la variable, N est l’ensemble en entrée et x <= 10 est un prédicat. Cela signifie que l’ensemble contient le double de tous les entiers naturels qui satisfont le prédicat.

Si nous voulions écrire cela en Haskell, nous pourrions le faire ainsi take 10 [2,4..]. Mais que faire si l’on ne voulait pas les doubles des 10 premiers entiers naturels, mais quelque chose de plus compliqué ? On pourrait utiliser une liste en compréhension pour ça. Les listes en compréhension sont très semblables aux ensembles en compréhension. Restons-en au cas des 10 entiers pairs pour l’instant. La liste de compréhension adéquate serait [x*2 | x <- [1..10]]. x est extrait de [1..10] et pour chaque élément de [1..10] (désormais attaché à x), nous prenons son double. En action.

ghci> [x*2 | x <- [1..10]]
[2,4,6,8,10,12,14,16,18,20]

Comme vous pouvez le voir, nous obtenons le résultat attendu. Ajoutons à présent une condition (ou un prédicat) à cette compréhension. Les prédicats se placent après les liaisons, et sont séparés de ceux-ci par une virgule. Disons que l’on cherche les éléments qui, une fois doublés, sont plus grands ou égaux à 12.

ghci> [x*2 | x <- [1..10], x*2 >= 12]
[12,14,16,18,20]

Cool, ça marche. Et si nous voulions tous les nombres de 50 à 100 dont le reste de la division par 7 est 3 ? Facile.

ghci> [ x | x <- [50..100], x `mod` 7 == 3]
[52,59,66,73,80,87,94]

Succès ! Notez que nettoyer une liste à l’aide de prédicats s’appelle aussi le filtrage. Nous avons pris une liste de nombres et l’avons filtrée en accord avec le prédicat. Un autre exemple. Disons qu’on veut une compréhension qui remplace chaque nombre impair plus grand que 10 par "BANG!" et chaque nombre impair plus petit que 10 par "BOOM!". Si un nombre est pair, on le rejette de la liste. Pour plus de facilité, on va placer cette compréhension dans une fonction, pour pouvoir la réutiliser facilement.

boomBangs xs = [ if x < 10 then "BOOM!" else "BANG!" | x <- xs, odd x]

La dernière partie de la compréhension est le prédicat. La fonction odd renvoie True pour un nombre impair, et False pour un nombre pair. L’élément est inclus dans la liste seulement si tous les prédicats sont évalués à True.

ghci> boomBangs [7..13]
["BOOM!","BOOM!","BANG!","BANG!"]

On peut inclure plusieurs prédicats. Si nous voulions tous les nombres de 10 à 20 qui sont différents de 13, 15 et 19, on pourrait faire :

ghci> [ x | x <- [10..20], x /= 13, x /= 15, x /= 19]
[10,11,12,14,16,17,18,20]

Non seulement on peut avoir plusieurs prédicats dans une liste en compréhension (un élément doit satisfaire tous les prédicats pour être inclus dans la liste résultante), mais on peut également piocher dans plusieurs listes. Lorsqu’on pioche dans plusieurs listes, les compréhensions produisent toutes les combinaisons des listes en entrée et joignent tout ça à l’aide de la fonction que l’on fournit. Une liste produite par une compréhension qui pioche dans deux listes de longueur 4 aura donc pour longueur 16, si tant est qu’on ne filtre pas d’élément. Si l’on a deux listes, [2, 5, 10] et [8, 10, 11], et qu’on veut les produits possibles des combinaisons de deux nombres de chacune de ces listes, voilà ce qu’on écrit :

ghci> [ x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]

Comme prévu, la longueur de la nouvelle liste est 9. Et si l’on voulait seulement les produits supérieurs à 50 ?

ghci> [ x*y | x <- [2,5,10], y <- [8,10,11], x*y > 50]
[55,80,100,110]

Pourquoi pas une compréhension qui combine une liste d’adjectifs et une liste de noms… pour provoquer une hilarité épique.

ghci> let nouns = ["hobo","frog","pope"]
ghci> let adjectives = ["lazy","grouchy","scheming"]
ghci> [adjective ++ " " ++ noun | adjective <- adjectives, noun <- nouns]
["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog",
"grouchy pope","scheming hobo","scheming frog","scheming pope"]

Je sais ! Écrivons notre propre version de length ! Appelons-la length'.

length' xs = sum [1 | _ <- xs]

_ signifie que l’on se fiche de ce qu’on a pioché dans la liste, donc plutôt que d’y donner un nom qu’on n’utilisera pas, on écrit _. Cette fonction remplace chaque élément de la liste par un 1, et somme cette liste. La somme résultante sera donc la longueur de la liste.

Un rappel amical : puisque les chaînes de caractères sont des listes, on peut utiliser les listes en compréhension pour traiter et produire des chaînes de caractères. Voici une fonction qui prend une chaîne de caractères et supprime tout sauf les caractères en majuscule.

removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]

Testons :

ghci> removeNonUppercase "Hahaha! Ahahaha!"
"HA"
ghci> removeNonUppercase "IdontLIKEFROGS"
"ILIKEFROGS"

Le prédicat ici fait tout le travail. Il indique que le caractère est inclus dans la nouvelle liste uniquement s’il appartient à la liste ['A'..'Z']. Il est possible d’imbriquer les compréhensions si vous opérez sur des listes qui contiennent des listes. Soit une liste qui contient plusieurs listes de nombres. Supprimons tous les nombres impairs sans aplatir la liste.

ghci> let xxs = [[1,3,5,2,3,1,2,4,5],[1,2,3,4,5,6,7,8,9],[1,2,4,2,1,6,3,1,3,2,3,6]]
ghci> [ [ x | x <- xs, even x ] | xs <- xxs]
[[2,2,4],[2,4,6,8],[2,4,2,6,2,6]]

Vous pouvez écrire les compréhensions de listes sur plusieurs lignes. Donc, en dehors de GHCi, il vaut mieux les découper sur plusieurs lignes, surtout si elles sont imbriquées.

Tuples

D’une façon, les tuples sont comme des listes - ils permettent de stocker plusieurs valeurs dans une seule. Cependant, il y a des différences fondamentales. Une liste de nombres est une liste de nombres. C’est son type, et cela n’importe pas qu’elle ait un seul nombre ou une infinité. Les tuples, par contre, sont utilisés lorsque vous savez exactement combien de valeurs vous désirez combiner, et son type dépend du nombre de composantes qu’il a et du type de ces composantes. Ils sont dénotés avec des parenthèses, et les composantes sont séparées par des virgules.

Une autre différence clé est qu’ils n’ont pas à être homogènes. Contrairement à une liste, un tuple peut contenir une combinaison de différents types.

Demandez-vous comment on représenterait un vecteur bidimensionnel en Haskell. Une possibilité serait d’utiliser une liste. Ça marcherait en partie. Que faire si l’on voulait mettre quelques vecteurs dans une liste pour représenter les points d’une forme du plan ? On pourrait faire [[1, 2], [8, 11], [4, 5]]. Le problème de cette méthode est que l’on pourrait également faire [[1, 2], [8, 11, 5], [4, 5]], qu’Haskell accepterait puisque cela reste une liste de listes de nombres, mais ça n’a pas vraiment de sens. Alors qu’un tuple de taille deux (aussi appelé un couple) est un type propre, ce qui signifie qu’une liste ne peut pas avoir quelques couples puis un triplet (tuple de taille trois), utilisons donc cela en lieu et place. Plutôt que d’entourer nos vecteurs de crochets, on utilise des parenthèses : [(1, 2), (8, 11), (4, 5)]. Et si l’on essayait d’entrer la forme [(1, 2), (8, 11, 5), (4, 5)] ? Eh bien, on aurait cette erreur :

Couldn't match expected type `(t, t1)'
against inferred type `(t2, t3, t4)'
In the expression: (8, 11, 5)
In the expression: [(1, 2), (8, 11, 5), (4, 5)]
In the definition of `it': it = [(1, 2), (8, 11, 5), (4, 5)]

Cela nous dit que l’on a essayé d’utiliser un couple et un triplet dans la même liste, ce qui ne doit pas arriver. Vous ne pourriez pas non plus créer une liste [(1, 2), ("One", 2)] car le premier élément de cette liste est un couple de nombres alors que le second est un couple d’une chaîne de caractères et d’un nombre. Les tuples peuvent aussi être utilisés pour représenter un grand éventail de données. Par exemple, si nous voulions représenter le nom et l’âge d’une personne en Haskell, on pourrait utiliser le triplet : ("Christopher", "Walken", 55). Comme dans l’exemple, les tuples peuvent aussi contenir des listes.

Utilisez des tuples lorsque vous savez à l’avance combien de composantes une donnée doit avoir. Les tuples sont beaucoup plus rigides car chaque taille de tuple a son propre type, donc on ne peut pas écrire une fonction générique pour ajouter un élément à un tuple - il faudrait écrire une fonction pour ajouter à un couple, une fonction pour ajouter à un triplet, un fonction pour ajouter à un quadruplet, etc.

Bien qu’il y ait des listes singleton, il n’existe pas de tuple singleton. Ça n’a pas beaucoup de sens si vous y réfléchissez. Un tuple singleton serait seulement la valeur qu’il contient, et n’aurait donc pas d’intérêt.

Comme les listes, les tuples peuvent être comparés entre eux si leurs composantes peuvent être comparées. Seulement, vous ne pouvez pas comparer des tuples de tailles différentes, alors que vous pouvez comparer des listes de tailles différentes. Deux fonctions utiles qui opèrent sur des couples :

fst prend un couple et renvoie sa première composante.

ghci> fst (8,11)
8
ghci> fst ("Wow", False)
"Wow"

snd prend un couple et renvoie sa seconde composante. Quelle surprise !

ghci> snd (8,11)
11
ghci> snd ("Wow", False)
False

Une fonction cool qui produit une liste de couples : zip. Elle prend deux listes et les zippe ensemble en joignant les éléments correspondants en des couples. C’est une fonction très simple, mais elle sert beaucoup. C’est particulièrement utile pour combiner deux listes d’une façon ou traverser deux listes simultanément. Démonstration.

ghci> zip [1,2,3,4,5] [5,5,5,5,5]
[(1,5),(2,5),(3,5),(4,5),(5,5)]
ghci> zip [1 .. 5] ["one", "two", "three", "four", "five"]
[(1,"one"),(2,"two"),(3,"three"),(4,"four"),(5,"five")]

Elle couple les éléments et produit une nouvelle liste. Le premier élément va avec le premier, le deuxième avec le deuxième, etc. Remarquez que, puisque les couples peuvent avoir différents types en elles, zip peut prendre deux listes qui contiennent des éléments de différents types et les zipper. Que se passe-t-il si les longueurs des listes ne correspondent pas ?

ghci> zip [5,3,2,6,2,7,2,5,4,6,6] ["im","a","turtle"]
[(5,"im"),(3,"a"),(2,"turtle")]

La liste la plus longue est simplement coupée pour correspondre à la longueur de la plus courte. Puisqu’Haskell est paresseux, on peut zipper des listes finies avec des listes infinies :

ghci> zip [1..] ["apple", "orange", "cherry", "mango"]
[(1,"apple"),(2,"orange"),(3,"cherry"),(4,"mango")]

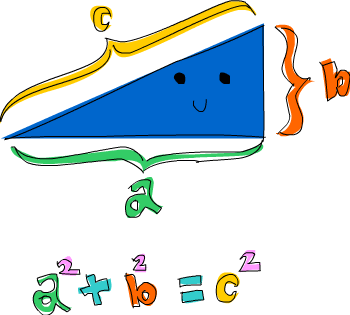
Voici un problème qui combine tuples et listes en compréhensions : quel triangle rectangle a des côtés tous entiers, tous inférieurs ou égaux à 10, et a un périmètre de 24 ? Premièrement, essayons de générer tous les triangles dont les côtés sont inférieurs ou égaux à 10 :

ghci> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10] ]

On pioche simplement dans trois listes et notre fonction de sortie combine les trois valeurs en triplets. Si vous évaluez en le tapant triangles, dans GHCi, vous obtiendrez tous les triangles possibles dont les côtés sont inférieurs ou égaux à 10. Ensuite, ajoutons une condition, que ceux-ci soient rectangles. On va également exploiter le fait que b est plus petit que l’hypoténuse et que le côté a est plus petit que b.

ghci> let rightTriangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2]

Nous y sommes presque. Maintenant, il ne reste plus qu’à modifier la fonction en disant que l’on veut ceux dont le périmètre est 24.

ghci> let rightTriangles' = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2, a+b+c == 24]
ghci> rightTriangles'
[(6,8,10)]

Et voilà notre réponse ! C’est un schéma courant en programmation fonctionnelle. Vous prenez un ensemble de solutions, et vous appliquez des transformations sur ces solutions et les filtrez jusqu’à obtenir les bonnes.