Quand on a parlé pour la première fois des foncteurs, on a vu que c’était un concept utile pour les valeurs sur lesquelles on pouvait mapper. Puis, on a poussé ce concept un cran plus loin en introduisant les foncteurs applicatifs, qui nous permettent de voir les valeurs de certains types de données comme des valeurs dans des contextes et d’utiliser des fonctions normales sur ces valeurs tout en préservant la sémantique de ces contextes.

Dans ce chapitre, nous allons découvrir les monades, qui sont juste des foncteurs applicatifs gonflés aux hormones, tout comme les foncteurs applicatifs étaient juste des foncteurs gonflés aux hormones.

Quand on a débuté les foncteurs, on a vu qu’il était possible de mapper des fonctions sur divers types de données. On a vu qu’à cet effet, la classe de types Functor avait été introduite, et cela a soulevé la question : quand on a une fonction de type a -> b et un type de données f a, comment mapper cette fonction sur le type de données pour obtenir un f b ? On a vu comment mapper quelque chose sur un Maybe a, une liste [a], une action I/O IO a, etc. On a même vu comment mapper une fonction a -> b sur d’autres fonctions de type r -> a pour obtenir des fonctions r -> b. Pour répondre à la question de comment mapper une fonction sur un type de données, tout ce qu’il nous a fallu considérer était le type de fmap :

fmap :: (Functor f) => (a -> b) -> f a -> f b

Puis, à le faire marcher pour notre type de données en écrivant l’instance de Functor appropriée.

Puis, on a vu une amélioration possible des foncteurs, et nous nous sommes dit, hé, et si cette fonction a -> b était déjà enveloppée dans une valeur fonctorielle ? Comme par exemple, si l’on avait Just (*3), comment appliquer cela à Just 5 ? Et si l’on voulait l’appliquer non pas à Just 5, mais plutôt à Nothing ? Ou si l’on avait [(*2), (+4)], comment l’appliquerions-nous à [1, 2, 3] ? Comment cela marcherait-il ? Pour cela, la classe de types Applicative est introduite, afin de répondre au problème à l’aide du type :

(<*>) :: (Applicative f) => f (a -> b) -> f a -> f b

On a aussi vu que l’on pouvait prendre une valeur normale et l’envelopper dans un type de données. Par exemple, on peut prendre un 1 et l’envelopper de manière à ce qu’il devienne un Just 1. On en faire un [1]. Ou une action I/O qui ne fait rien, mais retourne 1. La fonction qui fait cela s’appelle pure.

Comme on l’a dit, une valeur applicative peut être vue comme une valeur avec un contexte. Une valeur spéciale en gros. Par exemple, le caractère 'a' est un caractère normal, alors que Just 'a' a un contexte additionnel. Au lieu d’être un Char, c’est un Maybe Char, ce qui nous indique que sa valeur peut être un caractère, mais qu’il aurait aussi pu être absent.

La classe de types Applicative nous permettait d’utiliser des fonctions normales sur des valeurs dans des contextes tout en préservant le contexte de façon très propre. Observez :

ghci> (*) <$> Just 2 <*> Just 8
Just 16
ghci> (++) <$> Just "klingon" <*> Nothing
Nothing
ghci> (-) <$> [3,4] <*> [1,2,3]
[2,1,0,3,2,1]

Ah, cool, à présent qu’on les traite comme des valeurs applicatives, les valeurs Maybe a représentent des calculs qui peuvent avoir échoué, les valeurs [a] représentent des calculs qui ont plusieurs résultats (calculs non déterministes), les IO a représentent des valeurs qui ont des effets de bord, etc.

Les monades sont une extension naturelle des foncteurs applicatifs, et avec elles on cherche à résoudre ceci : si vous avez une valeur dans un contexte, m a, comment appliquer dessus une fonction qui prend une valeur normale a et retourne une valeur dans un contexte ? C’est-à-dire, comment appliquer une fonction de type a -> m b à une valeur de type m a ? En gros, on veut cette fonction :

(>>=) :: (Monad m) => m a -> (a -> m b) -> m b

Si l’on a une valeur spéciale, et une fonction qui prend une valeur normale mais retourne une valeur spéciale, comment donner la valeur spéciale à cette fonction ? C’est la question à laquelle on s’attaquera en étudiant les monades. On écrit m a plutôt que f a parce que le m signifie Monad, mais les monades sont seulement des foncteurs applicatifs supportant (>>=). La fonction (>>=) est prononcée bind (NDT : en français, cela signifie lier).

Quand on a une valeur normale a et une fonction normale a -> b, il est très facile d’alimenter la fonction avec la valeur - on applique simplement la fonction avec la valeur et voilà. Mais quand on a affaire à des valeurs qui viennent de certains contextes, il faut un peu plus y réfléchir pour voir comment ces valeurs spéciales peuvent être données aux fonctions, et comment prendre en compte leur comportement, mais vous verrez que c’est simple comme bonjour.

Trempons-nous les pieds avec Maybe

Maintenant qu’on a une vague idée de ce que sont les monades, voyons si l’on peut éclaircir cette notion un tant soit peu.

Sans surprise, Maybe est une monade, alors explorons cela encore un peu et voyons si l’on peut combiner cela avec ce qu’on sait des monades.

Une valeur ayant pour type Maybe a représente une valeur de type a avec le contexte de l’échec potentiel attaché. Une valeur Just "dharma" signifie que la chaîne de caractères "dharma" est présente, alors qu’une valeur Nothing représente son absence, ou si vous imaginez la chaîne de caractères comme le résultat d’un calcul, cela signifie que le calcul a échoué.

Quand on a regardé Maybe comme un foncteur, on a vu que si l’on veut fmap une fonction sur celui-ci, elle est mappée sur ce qui est à l’intérieur des valeurs Just, les Nothing étant conservés tels quels parce qu’il n’y a pas de valeur sur laquelle mapper !

Ainsi :

ghci> fmap (++"!") (Just "wisdom")
Just "wisdom!"
ghci> fmap (++"!") Nothing
Nothing

En tant que foncteur applicatif, cela fonctionne similairement. Cependant, les foncteurs applicatifs prennent une fonction enveloppée. Maybe est un foncteur applicatif de manière à ce que lorsqu’on utilise <*> pour appliquer une fonction dans un Maybe à une valeur dans un Maybe, elles doivent toutes deux être des valeurs Just pour que le résultat soit une valeur Just, autrement le résultat est Nothing. C’est logique, puisque s’il vous manque soit la fonction, soit son paramètre, vous ne pouvez pas l’inventer, donc vous devez propager l’échec :

ghci> Just (+3) <*> Just 3
Just 6
ghci> Nothing <*> Just "greed"
Nothing
ghci> Just ord <*> Nothing
Nothing

Quand on utilise le style applicatif pour appliquer des fonctions normales sur des valeurs Maybe, c’est similaire. Toutes les valeurs doivent être des Just, sinon le tout est Nothing !

ghci> max <$> Just 3 <*> Just 6
Just 6
ghci> max <$> Just 3 <*> Nothing
Nothing

À présent, pensons à ce que l’on ferait pour faire >>= sur Maybe. Comme on l’a dit, >>= prend une valeur monadique, et une fonction qui prend une valeur normale et retourne une valeur monadique, et parvient à appliquer cette fonction à la valeur monadique. Comment fait-elle cela, si la fonction n’accepte qu’une valeur normale ? Eh bien, pour ce faire, elle doit prendre en compte le contexte de la valeur monadique.

Dans ce cas, >>= prendrait un Maybe a et une fonction de type a -> Maybe b et appliquerait la fonction au Maybe a. Pour comprendre comment elle fait cela, on peut utiliser notre intuition venant du fait que Maybe est un foncteur applicatif. Mettons qu’on ait une fonction \x -> Just (x + 1). Elle prend un nombre, lui ajoute 1 et l’enveloppe dans un Just :

ghci> (\x -> Just (x+1)) 1
Just 2
ghci> (\x -> Just (x+1)) 100
Just 101

Si on lui donne 1, elle s’évalue en Just 2. Si on lui donne le nombre 100, le résultat est Just 101. Très simple. Voilà l’obstacle : comment donner une valeur Maybe a cette fonction ? Si on pense à ce que fait Maybe en tant que foncteur applicatif, répondre est plutôt simple. Si on lui donne une valeur Just, elle prend ce qui est dans le Just et applique la fonction dessus. Si on lui donne un Nothing, hmm, eh bien, on a une fonction, mais rien pour l’appliquer. Dans ce cas, faisons juste comme avant et retournons Nothing.

Plutôt que de l’appeler >>=, appelons-la applyMaybe pour l’instant. Elle prend un Maybe a et une fonction et retourne un Maybe b, parvenant à appliquer la fonction sur le Maybe a. Voici le code :

applyMaybe :: Maybe a -> (a -> Maybe b) -> Maybe b
applyMaybe Nothing f  = Nothing
applyMaybe (Just x) f = f x

Ok, à présent jouons un peu. On va l’utiliser en fonction infixe pour que la valeur Maybe soit sur le côté gauche et la fonction sur la droite :

ghci> Just 3 `applyMaybe` \x -> Just (x+1)
Just 4
ghci> Just "smile" `applyMaybe` \x -> Just (x ++ " :)")
Just "smile :)"
ghci> Nothing `applyMaybe` \x -> Just (x+1)
Nothing
ghci> Nothing `applyMaybe` \x -> Just (x ++ " :)")
Nothing

Dans l’exemple ci-dessus, on voit que quand on utilisait applyMaybe avec une valeur Just et une fonction, la fonction était simplement appliquée dans le Just. Quand on essayait de l’utiliser sur un Nothing, le résultat était Nothing. Et si la fonction retourne Nothing ? Voyons :

ghci> Just 3 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Just 3
ghci> Just 1 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Nothing

Comme prévu. Si la valeur monadique à gauche est Nothing, le tout est Nothing. Et si la fonction de droite retourne Nothing, le résultat est également Nothing. C’est très similaire au cas où on utilisait Maybe comme foncteur applicatif et on obtenait un Nothing en résultat lorsqu’il y avait un Nothing quelque part.

Il semblerait que, pour Maybe, on ait trouvé un moyen de prendre une valeur spéciale et de la donner à une fonction qui prend une valeur normale et en retourne une spéciale. On l’a fait en gardant à l’esprit qu’une valeur Maybe représentait un calcul pouvant échouer.

Vous vous demandez peut-être à quoi bon faire cela ? On pourrait croire que les foncteurs applicatifs sont plus puissants que les monades, puisqu’ils nous permettent de prendre une fonction normale et de la faire opérer sur des valeurs dans des contextes. On verra que les monades peuvent également faire ça, car elles sont des améliorations des foncteurs applicatifs, et qu’elles peuvent également faire des choses cool dont les foncteurs applicatifs sont incapables.

On va revenir à Maybe dans une minute, mais d’abord, découvrons la classe des types monadiques.

La classe de types Monad

Tout comme les foncteurs ont la classe de types Functor et les foncteurs applicatifs ont la classe de types Applicative, les monades viennent avec leur propre classe de types : Monad ! Wow, qui l’eut cru ? Voici à quoi ressemble la classe de types :

class Monad m where
    return :: a -> m a

    (>>=) :: m a -> (a -> m b) -> m b

    (>>) :: m a -> m b -> m b
    x >> y = x >>= \_ -> y

    fail :: String -> m a
    fail msg = error msg

Commençons par la première ligne. Elle dit class Monad m where. Mais, attendez, n’avons-nous pas dit que les monades étaient des foncteurs applicatifs améliorés ? Ne devrait-il pas y avoir une contrainte de classe comme class (Applicative m) => Monad m where afin qu’un type doive être un foncteur applicatif pour être une monade ? Eh bien, ça devrait être le cas, mais quand Haskell a été créé, il n’est pas apparu à ses créateurs que les foncteurs applicatifs étaient intéressants pour Haskell, et donc ils n’étaient pas présents. Mais soyez rassuré, toute monade est un foncteur applicatif, même si la déclaration de classe Monad ne l’indique pas.

La première fonction de la classe de types Monad est return. C’est la même chose que pure, mais avec un autre nom. Son type est (Monad m) => a -> m a. Elle prend une valeur et la place dans un contexte minimal contenant cette valeur. En d’autres termes, elle prend une valeur et l’enveloppe dans une monade. Elle est toujours définie comme pure de la classe de types Applicative, ce qui signifie qu’on la connaît déjà. On a déjà utilisé return quand on faisait des entrées-sorties. On s’en servait pour prendre une valeur et créer une I/O factice, qui ne faisait rien de plus que renvoyer la valeur. Pour Maybe elle prend une valeur et l’enveloppe dans Just.

La prochaine fonction est >>=, ou bind. C’est comme une application de fonction, mais au lieu de prendre une valeur normale pour la donner à une fonction normale, elle prend une valeur monadique (dans un contexte) et alimente une fonction qui prend une valeur normale et retourne une valeur monadique.

Ensuite, il y a >>. On n’y prêtera pas trop attention pour l’instant parce qu’elle vient avec une implémentation par défaut, et qu’on ne l’implémente presque jamais quand on crée des instances de Monad.

La dernière fonction de la classe de types Monad est fail. On ne l’utilise jamais explicitement dans notre code. En fait, c’est Haskell qui l’utilise pour permettre les échecs dans une construction syntaxique pour les monades que l’on découvrira plus tard. Pas besoin de se préoccuper de fail pour l’instant.

À présent qu’on sait à quoi la classe de types Monad ressemble, regardons comment Maybe est instancié comme Monad !

instance Monad Maybe where
    return x = Just x
    Nothing >>= f = Nothing
    Just x >>= f  = f x
    fail _ = Nothing

return est identique à pure, pas besoin de réfléchir. On fait comme dans Applicative et on enveloppe la valeur dans Just.

La fonction >>= est identique à notre applyMaybe. Quand on lui donne un Maybe a, on se souvient du contexte et on retourne Nothing si la valeur à gauche est Nothing, parce qu’il n’y a pas de valeur sur laquelle appliquer la fonction. Si c’est un Just, on prend ce qui est à l’intérieur et on applique f dessus.

On peut jouer un peu avec la monade Maybe :

ghci> return "WHAT" :: Maybe String
Just "WHAT"
ghci> Just 9 >>= \x -> return (x*10)
Just 90
ghci> Nothing >>= \x -> return (x*10)
Nothing

Rien de neuf ou d’excitant à la première ligne puisqu’on a déjà utilisé pure avec Maybe et on sait que return est juste pure avec un autre nom. Les deux lignes suivantes présentent un peu mieux >>=.

Remarquez comment, lorsqu’on donne Just 9 à la fonction \x -> return (x*10), le x a pris la valeur 9 dans la fonction. Il semble qu’on ait réussi à extraire la valeur du contexte Maybe sans avoir recours à du filtrage par motif. Et on n’a pas perdu le contexte de notre valeur Maybe, parce que quand elle vaut Nothing, le résultat de >>= sera également Nothing.

Le funambule

À présent qu’on sait comment donner un Maybe a à une fonction ayant pour type a -> Maybe b tout en tenant compte du contexte de l’échec potentiel, voyons comment on peut utiliser >>= de manière répétée pour gérer le calcul de plusieurs valeurs Maybe a.

Pierre a décidé de faire une pause dans son emploi au centre de pisciculture pour s’adonner au funanbulisme. Il n’est pas trop mauvais, mais il a un problème : des oiseaux n’arrêtent pas d’atterrir sur sa perche d’équilibre ! Ils viennent se reposer un instant, discuter avec leurs amis aviaires, avant de décoller en quête de miettes de pain. Cela ne le dérangerait pas tant si le nombre d’oiseaux sur le côté gauche de la perche était égal à celui sur le côté droit. Mais parfois, tous les oiseaux décident qu’ils préfèrent le même côté, et ils détruisent son équilibre, l’entraînant dans une chute embarrassante (il a un filet de sécurité).

Disons qu’il arrive à tenir en équilibre tant que le nombre d’oiseaux sur les côtés gauche et droit ne s’éloignent pas de plus de trois. Ainsi, s’il y a un oiseau à droite et quatre oiseaux à gauche, tout va bien. Mais si un cinquième oiseau atterrit sur sa gauche, il perd son équilibre et plonge malgré lui.

Nous allons simuler des oiseaux atterrissant et décollant de la perche et voir si Pierre tient toujours après un certain nombre d’arrivées et de départs. Par exemple, on souhaite savoir ce qui arrive à Pierre si le premier oiseau arrive sur sa gauche, puis quatre oiseaux débarquent sur sa droite, et enfin l’oiseau sur sa gauche décide de s’envoler.

On peut représenter la perche comme une simple paire d’entiers. La première composante compte les oiseaux sur sa gauche, la seconde ceux sur sa droite :

type Birds = Int
type Pole = (Birds,Birds)

Tout d’abord, on crée un synonyme du type Int, appelé Birds, parce qu’on va utiliser des entiers pour représenter un nombre d’oiseaux. Puis, on crée un synonyme pour (Birds, Birds) qu’on appelle Pole (à ne pas confondre avec une personne d’origine polonaise).

Ensuite, pourquoi ne pas créer une fonction qui prenne un nombre d’oiseaux et les fait atterrir sur un côté de la perche ? Voici les fonctions :

landLeft :: Birds -> Pole -> Pole
landLeft n (left,right) = (left + n,right)

landRight :: Birds -> Pole -> Pole
landRight n (left,right) = (left,right + n)

Simple. Essayons-les :

ghci> landLeft 2 (0,0)
(2,0)
ghci> landRight 1 (1,2)
(1,3)
ghci> landRight (-1) (1,2)
(1,1)

Pour faire décoller les oiseaux, on a utilisé un nombre négatif. Puisque faire atterrir des oiseaux sur un Pole retourne un Pole, on peut chaîner les applications de landLeft et landRight :

ghci> landLeft 2 (landRight 1 (landLeft 1 (0,0)))
(3,1)

Quand on applique la fonction landLeft 1 sur (0, 0), on obtient (1, 0). Puis, on fait atterrir un oiseau sur le côté droit, ce qui donne (1, 1). Finalement, deux oiseaux atterrissent à gauche, donnant (3, 1). On applique une fonction en écrivant d’abord la fonction puis le paramètre, mais ici, il serait plus pratique d’avoir la perche en première et ensuite la fonction d’atterrissage. Si l’on crée une fonction :

x -: f = f x

On peut appliquer les fonctions en écrivant d’abord le paramètre puis la fonction :

ghci> 100 -: (*3)
300
ghci> True -: not
False
ghci> (0,0) -: landLeft 2
(2,0)

Ainsi, on peut faire atterrir de façon répétée des oiseaux, de manière plus lisible :

ghci> (0,0) -: landLeft 1 -: landRight 1 -: landLeft 2
(3,1)

Plutôt cool ! Cet exemple est équivalent au précédent où l’on faisait atterrir plusieurs fois des oiseaux sur la perche, mais il a l’air plus propre. Ici, il est plus facile de voir qu’on commence avec (0, 0) et qu’on fait atterrir un oiseau à gauche, puis un à droite, puis deux à gauche.

Jusqu’ici, tout est bien. Mais que se passe-t-il lorsque 10 oiseaux atterrissent du même côté ?

ghci> landLeft 10 (0,3)
(10,3)

10 oiseaux à gauche et seulement 3 à droite ? Avec ça, le pauvre Pierre est sûr de se casser la figure ! Ici, c’est facile de s’en rendre compte, mais si l’on avait une séquence comme :

ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)

On pourrait croire que tout va bien, mais si vous suivez attentivement les étapes, vous verrez qu’à un moment il y a 4 oiseaux sur la droite et aucun à gauche ! Pour régler ce problème, il faut retourner à nos fonctions landLeft et landRight. De ce qu’on voit, on veut que ces fonctions puissent échouer. C’est-à-dire, on souhaite qu’elles retournent une nouvelle perche tant que l’équilibre est respecté, mais qu’elles échouent si les oiseaux atterrissent en disproportion. Et quel meilleur moyen d’ajouter un contexte de possible échec que d’utiliser une valeur Maybe ? Reprenons ces fonctions :

landLeft :: Birds -> Pole -> Maybe Pole
landLeft n (left,right)
    | abs ((left + n) - right) < 4 = Just (left + n, right)
    | otherwise                    = Nothing

landRight :: Birds -> Pole -> Maybe Pole
landRight n (left,right)
    | abs (left - (right + n)) < 4 = Just (left, right + n)
    | otherwise                    = Nothing

Plutôt que de retourner un Pole, ces fonctions retournent un Maybe Pole. Elles prennent toujours un nombre d’oiseaux et une perche existante, mais elles vérifient si l’atterrisage des oiseaux déséquilibre ou non Pierre. On a utilisé des gardes pour vérifier si la différence entre les extrémités de la perche est inférieure à 4. Si c’est le cas, on enveloppe la nouvelle perche dans un Just et on la retourne. Sinon, on retourne Nothing pour indiquer l’échec.

Mettons ces nouvelles-nées à l’épreuve :

ghci> landLeft 2 (0,0)
Just (2,0)
ghci> landLeft 10 (0,3)
Nothing

Joli ! Quand on fait atterrir des oiseaux sans détruire l’équilibre de Pierre, on obtient une nouvelle perche encapsulée dans un Just. Mais quand trop d’oiseaux arrivent d’un côté de la perche, on obtient Nothing. C’est cool, mais on dirait qu’on a perdu la capacité de chaîner des atterissages d’oiseaux sur la perche. On ne peut plus faire landLeft 1 (landRight 1 (0,0)) parce que lorsqu’on applique landRight 1 à (0, 0), on n’obtient pas un Pole mais un Maybe Pole. landLeft 1 prend un Pole et retourne un Maybe Pole.

On a besoin d’une manière de prendre un Maybe Pole et de le donner à une fonction qui prend un Pole et retourne un Maybe Pole. Heureusement, on a >>=, qui fait exactement ça pour Maybe. Essayons :

ghci> landRight 1 (0,0) >>= landLeft 2
Just (2,1)

Souvenez-vous, landLeft 2 a pour type Pole -> Maybe Pole. On ne pouvait pas lui donner directement un Maybe Pole résultant de landRight 1 (0, 0), alors on utilise >>= pour prendre une valeur dans un contexte et la passer à landLeft 2. >>= nous permet en effet de traiter la valeur Maybe comme une valeur avec un contexte, parce que si l’on donne Nothing à landLeft 2, on obtient bien Nothing et l’échec est propagé :

ghci> Nothing >>= landLeft 2
Nothing

Ainsi, on peut à présent chaîner des atterrissages pouvant échouer parce que >>= nous permet de donner une valeur monadique à une fonction qui attend une valeur normale.

Voici une séquence d’atterrisages :

ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)

Au début, on utilise return pour prendre une perche et l’envelopper dans un Just. On aurait pu appeler directement landRight 2 sur (0, 0), c’était la même chose, mais la notation est plus consistente en utilisant >>= pour chaque fonction. Just (0, 0) alimente landRight 2, résultant en Just (0, 2). À son tour, alimentant landLeft 2, résultant en Just (2, 2), et ainsi de suite.

Souvenez-vous de l’exemple précédent où l’on introduisait la notion d’échec dans la routine de Pierre :

ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)

Cela ne simulait pas très bien son interaction avec les oiseaux, parce qu’au milieu, il perdait son équilibre, mais le résultat ne le reflétait pas. Redonnons une chance à cette fonction en utilisant l’application monadique (>>=) plutôt que l’application normale.

ghci> return (0,0) >>= landLeft 1 >>= landRight 4 >>= landLeft (-1) >>= landRight (-2)
Nothing

Génial. Le résultat final représente l’échec, qui est ce qu’on attendait. Regardons comment ce résultat est obtenu. D’abord, return place (0, 0) dans un contexte par défaut, en faisant un Just (0, 0). Puis, Just (0,0) >>= landLeft 1 a lieu. Puisque Just (0, 0) est une valeur Just, landLeft 1 est appliquée à (0, 0), retournant Just (1, 0), parce que l’oiseau seul ne détruit pas l’équilibre. Ensuite, Just (1,0) >>= landRight 4 prend place, et le résultat est Just (1, 4) car l’équilibre reste intact, bien qu’à sa limite. Just (1, 4) est donné à landLeft (-1). Cela signifie que landLeft (-1) (1, 4) prend place. Conformément au fonctionnement de landLeft, cela retourne Nothing, parce que la perche résultante est déséquilibrée. À présent on a un Nothing qui est donné à landRight (-2), mais parce que c’est un Nothing, le résultat est automatiquement Nothing, puisqu’on n’a rien sur quoi appliquer landRight (-2).

On n’aurait pas pu faire ceci en utilisant Maybe comme un foncteur applicatif. Si vous essayez, vous vous retrouverez bloqué, parce que les foncteurs applicatifs ne permettent pas que les valeurs applicatives interagissent entre elles. Au mieux, elles peuvent être utilisées en paramètre d’une fonction en utilisant le style applicatif. Les opérateurs applicatifs iront chercher leurs résultats, et les passer à la fonction de façon appropriée en fonction du foncteur applicatif, puis placeront les valeurs applicatives résultantes ensemble, mais il n’y aura que peu d’interaction entre elles. Ici, cependant, chaque étape dépend du résultat de la précédente. À chaque atterrissage, le résultat possible de l’atterrissage précédent est examiné pour voir l’équilibre de la perche. Cela détermine l’échec ou non de l’atterrissage.

On peut aussi créer une fonction qui ignore le nombre d’oiseaux sur la perche et fait tomber Pierre. On peut l’appeler banana :

banana :: Pole -> Maybe Pole
banana _ = Nothing

On peut maintenant la chaîner à nos atterrissages d’oiseaux. Elle causera toujours la chute de notre funambule, parce qu’elle ignore ce qu’on lui passe et retourne un échec. Regardez :

ghci> return (0,0) >>= landLeft 1 >>= banana >>= landRight 1
Nothing

La valeur Just (1, 0) est passée à banana, mais elle produit Nothing, ce qui force le tout à résulter en Nothing. Comme c’est triste !

Plutôt que de créer des fonctions qui ignorent leur entrée et retournent une valeur monadique prédéterminée, on peut utiliser la fonction >>, dont l’implémentation par défaut est :

(>>) :: (Monad m) => m a -> m b -> m b
m >> n = m >>= \_ -> n

Normalement, passer une valeur à une fonction qui ignore son paramètre et retourne tout le temps une valeur prédéterminée résulterait toujours en cette valeur prédéterminée. Avec les monades cependant, leur contexte et signification doit être également considéré. Voici comment >> agit sur Maybe :

ghci> Nothing >> Just 3
Nothing
ghci> Just 3 >> Just 4
Just 4
ghci> Just 3 >> Nothing
Nothing

Si vous remplacez >> par >>= \_ ->, il est facile de voir pourquoi cela arrive.

On peut remplacer notre fonction banana dans la chaîne par un >> suivi d’un Nothing :

ghci> return (0,0) >>= landLeft 1 >> Nothing >>= landRight 1
Nothing

Et voilà, échec évident garanti !

Il est aussi intéressant de regarder ce qu’on aurait dû écrire si l’on n’avait pas fait le choix astucieux de traiter les valeurs Maybe comme des valeurs dans un contexte pour les donner à nos fonctions. Voici à quoi une série d’atterrissages aurait ressemblé :

routine :: Maybe Pole
routine = case landLeft 1 (0,0) of
    Nothing -> Nothing
    Just pole1 -> case landRight 4 pole1 of
        Nothing -> Nothing
        Just pole2 -> case landLeft 2 pole2 of
            Nothing -> Nothing
            Just pole3 -> landLeft 1 pole3

On fait atterrir un oiseau à gauche, puis on examine les possibilités d’échec et de succès. Dans le cas d’un échec, on retourne Nothing. Dans le cas d’une réussite, on fait atterrir des oiseaux à droite et on répète le tout encore et encore. Convertir cette monstruosité en une jolie chaîne d’applications monadiques à l’aide de >>= est un exemple classique prouvant comment la monade Maybe nous sauve beaucoup de temps lorsqu’on doit effectuer des calculs successifs qui peuvent échouer.

Remarquez comme l’implémentation de >>= pour Maybe fait apparaître exactement la logique de vérifier si une valeur est Nothing, et quand c’est le cas, de retourner Nothing immédiatement, alors que quand ce n’est pas le cas, on continue avec ce qui est dans le Just.

Dans cette section, on a pris quelques fonctions qu’on avait et vu qu’elles pouvaient fonctionner encore mieux si les valeurs qu’elles retournaient supportaient la notion d’échec. En transformant ces valeurs en valeurs Maybe et en remplaçant l’application normale des fonctions par >>=, on a obtenu un mécanisme de propagation d’erreur presque sans effort, parce que >>= préserve le contexte des valeurs qu’elle applique aux fonctions. Dans ce cas, le contexte indiquait que nos valeurs pouvaient avoir échoué, et lorsqu’on appliquait nos fonctions sur ces valeurs, la possibilité d’échec était prise en compte.

Notation do

Les monades en Haskell sont tellement utiles qu’elles ont leur propre syntaxe spéciale appelée notation do. On a déjà rencontré la notation do quand on faisait des entrées-sorties, et on a alors dit qu’elle servait à coller plusieurs actions I/O en une seule. Eh bien, il s’avère que la notation do n’est pas seulement pour IO, mais peut être utilisée pour n’importe quelle monade. Le principe est identique : coller ensemble plusieurs valeurs monadiques en séquence. Nous allons regarder comment la notation do fonctionne et en quoi elle est utile.

Considérez l’exemple familier de l’application monadique :

ghci> Just 3 >>= (\x -> Just (show x ++ "!"))
Just "3!"

Déjà vu. Donner une valeur monadique à une fonction qui en retourne une autre, rien de grandiose. Remarquez comme en faisant ainsi, x devient 3 à l’intérieur de la lambda. Une fois dans la lambda, c’est juste une valeur normale plutôt qu’une valeur monadique. Et si l’on avait encore un >>= dans cette fonction ? Regardez :

ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Just "3!"

Ah, une utilisation imbriquée de >>= ! Dans la lambda la plus à l’extérieur, on donne Just "!" à la lambda \y -> Just (show x ++ y). Dans cette lambda là, le y devient "!", et le x est toujours 3 parce qu’on l’obtient de la lambda la plus englobante. Cela me rappelle un peu l’expression suivante :

ghci> let x = 3; y = "!" in show x ++ y
"3!"

La différence principale entre les deux, c’est que les valeurs dans la première sont monadiques. Ce sont des valeurs dans le contexte de l’échec. On peut remplacer n’importe laquelle d’entre elle par un échec :

ghci> Nothing >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Nothing >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Nothing))
Nothing

À la première ligne, donner Nothing à la fonction résulte naturellement en Nothing. À la deuxième ligne, on donne Just 3 à une fonction et x devient 3, mais ensuite on donne Nothing à la lambda intérieure, et le résultat est Nothing, ce qui cause la lamba extérieure à produire Nothing à son tour. C’est donc un peu comme assigner des valeurs à des variables dans des expressions let, seulement les valeurs sont monadiques.

Pour mieux illustrer ce point, écrivons un script dans lequel chaque Maybe prend une ligne :

foo :: Maybe String
foo = Just 3   >>= (\x ->
      Just "!" >>= (\y ->
      Just (show x ++ y)))

Pour nous éviter d’écrire ces énervantes lambdas successives, Haskell nous offre la notation do. Elle nous permet de réécrire le bout de code précédent ainsi :

foo :: Maybe String
foo = do
    x <- Just 3
    y <- Just "!"
    Just (show x ++ y)

Il semblerait qu’on ait gagné la capacité d’extraire temporairement des valeurs Maybe sans avoir à vérifier si elles sont des Just ou des Nothing à chaque étape. C’est cool ! Si n’importe laquelle des valeurs qu’on essaie d’extraire est Nothing, l’expression do entière retourne Nothing. On attrape les valeurs (potentiellement existantes) et on laisse >>= s’occuper du contexte de ces valeurs. Il est important de se rappeler que les expressions do sont juste une syntaxe différente pour chaîner les valeurs monadiques.

Dans une expression do, chaque ligne est une valeur monadique. Pour inspecter le résultat, on utilise <-. Si on a un Maybe String et qu’on le lie à une variable par <-, cette variable aura pour type String, tout comme, lorsqu’on utilisait >>= pour passer une valeur monadique à des lambdas. La dernière valeur monadique d’une expression do, comme Just (show x ++ y) ici, ne peut pas être utilisée avec <- pour lier son résultat, parce que cela ne serait pas logique si l’on traduisait à nouveau le do en chaînes d’applications avec >>=. Plutôt, le résultat de cette dernière expression est le résultat de la valeur monadique entière, prenant en compte l’échec possible des précédentes.

Par exemple, examinez la ligne suivante :

ghci> Just 9 >>= (\x -> Just (x > 8))
Just True

Puisque le paramètre de gauche de >>= est une valeur Just, la lambda est appliquée à 9 et le résultat est Just True. Si l’on réécrit cela en notation do, on obtient :

marySue :: Maybe Bool
marySue = do
    x <- Just 9
    Just (x > 8)

Si l’on compare les deux, il est facile de comprendre pourquoi le résultat de la valeur monadique complète est celui de la dernière valeur monadique écrite dans l’expression do, après avoir chaîné toutes les précédentes.

La routine de notre funambule peut être exprimée avec la notation do. landLeft et landRight prennent un nombre d’oiseaux et une perche et produisent une perche enveloppée dans un Just, à moins que le funambule ne glisse, auquel cas Nothing est produit. On a utilisé >>= pour chaîner les étapes successives parce que chacune d’elles dépendait de la précédente, et chacune ajoutait un contexte d’échec éventuel. Voici deux oiseaux atterrissant à gauche, suivis de deux oiseaux à droite et d’un autre à gauche :

routine :: Maybe Pole
routine = do
    start <- return (0,0)
    first <- landLeft 2 start
    second <- landRight 2 first
    landLeft 1 second

Voyons si cela réussit :

ghci> routine
Just (3,2)

Oui ! Bien. Quand nous faisions ces routines explicitement avec >>=, on faisait souvent quelque chose comme return (0, 0) >>= landLeft 2, parce que landLeft 2 est une fonction qui retourne une valeur Maybe. Avec les expressions do cependant, chaque ligne doit comporter une valeur monadique. Il faut donc passer explicitement le Pole précédent aux fonctions landLeft et landRight. Si l’on examinait les variables auxquelles on a lié nos valeurs Maybe, start vaudrait (0, 0), first vaudrait (2, 0), et ainsi de suite.

Puisque les expressions do sont écrites ligne par ligne, elles peuvent avoir l’air de code impératif pour certaines personnes. Mais en fait, elles sont seulement séquentielles, puisque chaque valeur de chaque ligne dépend du résultat des précédentes, ainsi que de leur contexte (dans ce cas, savoir si elles ont réussi ou échoué).

Encore une fois, regardons à quoi ressemblerait le code si nous n’avions pas utilisé les aspects monadiques de Maybe :

routine :: Maybe Pole
routine =
    case Just (0,0) of
        Nothing -> Nothing
        Just start -> case landLeft 2 start of
            Nothing -> Nothing
            Just first -> case landRight 2 first of
                Nothing -> Nothing
                Just second -> landLeft 1 second

Voyez comme dans le cas d’un succès, le tuple à l’intérieur de Just (0, 0) devient start, le résultat de landLeft 2 start devient first, etc.

Si l’on veut lancer à Pierre une peau de banane avec la notation do, on peut le faire ainsi :

routine :: Maybe Pole
routine = do
    start <- return (0,0)
    first <- landLeft 2 start
    Nothing
    second <- landRight 2 first
    landLeft 1 second

Quand on écrit une ligne en notation do sans lier sa valeur monadique avec <-, c’est comme si l’on avait mis >> après la valeur monadique dont on souhaite ignorer le résultat. On séquence la valeur monadique mais on ignore son résultat parce qu’on s’en fiche, et parce que c’est plus joli que d’écrire _ <- Nothing, qui est équivalent.

À vous de choisir quand utiliser la notation do et quand utiliser explicitement >>=. Je pense que cet exemple se prête plus à l’utilisation explicite de >>= parce que chaque étape ne nécessite spécifiquement que le résultat de la précédente. Avec la notation do, il a fallu écrire à chaque fois sur quelle perche les oiseaux atterrissaient, mais c’était à chaque fois celle qui précédait immédiatement. Cependant, cela a fondé notre intuition de la notation do.

Avec la notation do, lorsqu’on lie des valeurs monadiques à des noms, on peut utiliser du filtrage par motif, tout comme dans les expressions let et les paramètres de fonctions. Voici un exemple de filtrage par motif dans une expression do :

justH :: Maybe Char
justH = do
    (x:xs) <- Just "hello"
    return x

On utilise le filtrage par motif pour obtenir le premier caractère de la chaîne "hello" et on la présente comme résultat. Ainsi, justH est évalué en Just 'h'.

Mais si ce filtrage par motif échoue ? Quand un filtrage par motif dans une fonction échoue, le prochain motif est essayé. Si le filtrage parcourt tous les motifs de la fonction donnée sans succès, une erreur est levée et notre programme plante. D’un autre côté, un échec de filtrage par motif dans une expression let résulte en une erreur immédiate, parce qu’elles n’ont pas de mécanisme de motif suivant. Quand un filtrage par motif échoue dans une expression do, la fonction fail est appelée. Elle fait partie de la classe de types Monad et permet à un filtrage par motif échoué de résulter en un échec dans le contexte de cette monade, plutôt que de planter notre programme. Son implémentation par défaut est :

fail :: (Monad m) => String -> m a
fail msg = error msg

Donc, par défaut, elle plante notre programme, mais les monades qui contiennent un contexte d’échec éventuel (comme Maybe) implémentent généralement leur propre version. Pour Maybe, elle est implémentée ainsi :

fail _ = Nothing

Elle ignore le message et crée un Nothing. Ainsi, quand le filtrage par motif échoue pour une valeur Maybe dans une notation do, la valeur de la monade entière est Nothing. C’est préférable à un plantage du programme. Voici une expression do avec un motif voué à l’échec :

wopwop :: Maybe Char
wopwop = do
    (x:xs) <- Just ""
    return x

Le filtrage par motif échoue, donc l’effet est le même que si la ligne entière comprenant le motif était remplacée par Nothing. Essayons :

ghci> wopwop
Nothing

Le motif échoué a provoqué l’échec dans le contexte de la monade plutôt que de provoquer un échec du programme entier, ce qui est plutôt sympa.

La monade des listes

Jusqu’ici, on a vu comment les valeurs Maybe pouvaient être vues comme des valeurs dans un contexte d’échec, et comment incorporer la gestion d’erreur dans notre code en utilisant >>= pour alimenter les fonctions. Dans cette section, on va voir comment utiliser les aspects monadiques des listes pour introduire le non déterminisme dans notre code de manière claire et lisible.

On a déjà parlé du fait que les listes représentent des valeurs non déterministes quand elles sont utilisées comme foncteurs applicatifs. Une valeur comme 5 est déterministe. Elle n’a qu’un résultat, et on sait exactement lequel c’est. D’un autre côté, une valeur comme [3, 8, 9] contient plusieurs résultats, on peut donc la voir comme une valeur qui est en fait plusieurs valeurs à la fois. Utiliser les listes comme des foncteurs applicatifs démontre ce non déterminisme élégamment :

ghci> (*) <$> [1,2,3] <*> [10,100,1000]
[10,100,1000,20,200,2000,30,300,3000]

Toutes les combinaisons possibles de multiplication d’un élément de la liste de gauche par un élément de la liste de droite sont inclues dans la liste résultante. Quand on fait du non déterminisme, il y a beaucoup de choix possibles, donc on les essaie tous, et le résultat est également une valeur non déterministe, avec encore plus de résultats.

Ce contexte de non déterminisme se transfère très joliment aux monades. Regardons immédiatement l’instance de Monad pour les listes :

instance Monad [] where
    return x = [x]
    xs >>= f = concat (map f xs)
    fail _ = []

return fait la même chose que pure, on est donc déjà familiarisé avec return pour les listes. Elle prend une valeur et la place dans un contexte par défaut minimal retournant cette valeur. En d’autres termes, elle crée une liste qui ne contient que cette valeur comme résultat. C’est utile lorsque l’on veut envelopper une valeur normale dans une liste afin qu’elle puisse interagir avec des valeurs non déterministes.

Pour comprendre comment >>= fonctionne pour les listes, il vaut mieux la voir en action pour développer notre intuition d’abord. >>= consiste à prendre une valeur dans un contexte (une valeur monadique) et la donner à une fonction qui prend une valeur normale et en retourne une dans un contexte. Si cette fonction produisait simplement une valeur normale plutôt qu’une dans un contexte, >>= ne nous serait pas très utile parce qu’après une utilisation, le contexte serait perdu. Essayons donc de donner une valeur non déterministe à une fonction.

ghci> [3,4,5] >>= \x -> [x,-x]
[3,-3,4,-4,5,-5]

Quand on utilisait >>= avec Maybe, la valeur monadique était passée à la fonction en prenant en compte le possible échec. Ici, elle prend en compte le non déterminisme pour nous. [3, 4, 5] est une valeur non déterministe et on la donne à une fonction qui retourne également une valeur non déterministe. Le résultat est également non déterministe, et contient tous les résultats possibles consistant à prendre un élément de la liste [3, 4, 5] et de le passer à la fonction \x -> [x, -x]. Cette fonction prend un nombre et produit deux résultats : le nombre inchangé et son opposé. Ainsi, quand on utilise >>= pour donner cette liste à la fonction, chaque nombre est gardé inchangé et opposé. Le x de la lambda prend chaque valeur de la liste qu’on donne à la fonction.

Pour voir comment cela a lieu, on peut simplement suivre l’implémentation. D’abord, on commence avec la liste [3, 4, 5]. Puis, on mappe la lambda sur la liste, et le résultat est :

[[3,-3],[4,-4],[5,-5]]

La lambda est appliquée à chaque élément et on obtient une liste de listes. Finalement, on aplatit la liste, et voilà ! Nous avons appliqué une fonction non déterministe à une valeur non déterministe !

Le non déterminisme supporte également l’échec. La liste vide [] est presque l’équivalent de Nothing, parce qu’elle signifie l’absence de résultat. C’est pourquoi l’échec est défini comme la liste vide. Le message d’erreur est jeté. Jouons avec des listes qui échouent :

ghci> [] >>= \x -> ["bad","mad","rad"]
[]
ghci> [1,2,3] >>= \x -> []
[]

À la première ligne, une liste vide est donnée à la lambda. Puisque la liste n’a pas d’éléments, aucun élément ne peut être passé à la fonction et ainsi le résultat est une liste vide. C’est similaire à donner Nothing à une fonction. À la seconde ligne, chaque élément est passé à la fonction, mais l’élément est ignoré et la fonction retourne une liste vide. Parce que la fonction échoue quelle que soit son entrée, le résultat est un échec.

Tout comme les valeurs Maybe, on peut chaîner plusieurs listes avec >>=, propageant le non déterminisme :

ghci> [1,2] >>= \n -> ['a','b'] >>= \ch -> return (n,ch)
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]

La liste [1, 2] est liée à n et ['a', 'b'] est liée à ch. Puis, on fait return (n, ch) (ou [(n, ch)]), ce qui signifie prendre une paire (n, ch) et la placer dans un contexte minimal. Dans ce cas, c’est la liste la plus petite contenant la valeur (n, ch) et étant le moins non déterministe possible. Son effet sur le contexte est donc minimal. Ce qu’on dit ici, c’est : pour chaque élément dans [1, 2], et pour chaque élément de ['a', 'b'], produis un tuple d’un élément de chaque liste.

En général, parce que return prend une valeur et l’enveloppe dans un contexte minimal, elle n’a pas d’effet additionnel (comme l’échec pour Maybe, ou ajouter du non déterminisme pour les listes), mais présente tout de même quelque chose en résultat.

Voici l’exemple précédent réécrit avec la notation do :

listOfTuples :: [(Int,Char)]
listOfTuples = do
    n <- [1,2]
    ch <- ['a','b']
    return (n,ch)

Cela rend un peu plus évident le fait que n prenne chaque valeur dans [1, 2] et ch chaque valeur de ['a', 'b']. Tout comme avec Maybe, on extrait des éléments de valeurs monadiques, et on les traite comme des valeurs normales, et >>= s’occupe du contexte pour nous. Le contexte dans ce cas est le non déterminisme.

Utiliser les listes avec la notation do me rappelle quelque chose qu’on a déjà vu. Regardez le code suivant :

ghci> [ (n,ch) | n <- [1,2], ch <- ['a','b'] ]
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]

Oui ! Les listes en compréhension ! Dans notre exemple avec la notation do, n prenait chaque résultat de [1, 2], et pour chacun d’eux, ch recevait un résultat de ['a', 'b'], et enfin la dernière ligne plaçait (n, ch) dans un contexte par défaut (une liste singleton) pour le présenter comme résultat sans introduire plus de non déterminisme. Dans cette liste en compréhension, la même chose a lieu, mais on n’a pas eu à écrire return à la fin pour présenter (n, ch) comme le résultat, parce que la fonction de sortie de la compréhension de liste s’en occupe pour nous.

En fait, les listes en compréhension sont juste un sucre syntaxique pour utiliser les listes comme des monades. Au final, les listes en compréhension, ainsi que les listes en notation do, sont traduites en utilisations de >>= pour faire les calculs non déterministes.

Les listes en compréhension nous permettent de filtrer la sortie. Par exemple, on peut filtrer une liste de nombres pour chercher seulement ceux qui contiennent le chiffre 7 :

ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]

On applique show à x pour transformer notre nombre en chaîne de caractères, et on vérifie si le caractère 7 fait partie de cette chaîne. Plutôt malin. Pour voir comment le filtrage dans les listes en compréhension se traduit dans la monade des listes, il nous faut regarder la fonction guard et la classe de types MonadPlus. La classe de types MonadPlus est pour les monades qui peuvent aussi se comporter en monoïdes. Voici sa définition :

class Monad m => MonadPlus m where
    mzero :: m a
    mplus :: m a -> m a -> m a

mzero est synonyme de mempty de la classe de types Monoid, et mplus correspond à mappend. Parce que les listes sont des monoïdes ainsi que des monades, elles peuvent être instance de cette classe de types :

instance MonadPlus [] where
    mzero = []
    mplus = (++)

Pour les listes, mzero représente un calcul non déterministe qui n’a pas de résultats - un calcul échoué. mplus joint deux valeurs non déterministes en une. La fonction guard est définie ainsi :

guard :: (MonadPlus m) => Bool -> m ()
guard True = return ()
guard False = mzero

Elle prend une valeur booléenne et si c’est True, elle prend un () et le place dans un contexte minimal par défaut qui réussisse toujours. Sinon, elle crée une valeur monadique échouée. La voici en action :

ghci> guard (5 > 2) :: Maybe ()
Just ()
ghci> guard (1 > 2) :: Maybe ()
Nothing
ghci> guard (5 > 2) :: [()]
[()]
ghci> guard (1 > 2) :: [()]
[]

Ça a l’air intéressant, mais comment est-ce utile ? Dans la monade des listes, on l’utilise pour filtrer des calculs non déterministes. Observez :

ghci> [1..50] >>= (\x -> guard ('7' `elem` show x) >> return x)
[7,17,27,37,47]

Le résultat ici est le même que le résultat de la liste en compréhension précédente. Comment guard fait-elle cela ? Regardons d’abord comment elle fonctionne en conjonction avec >> :

ghci> guard (5 > 2) >> return "cool" :: [String]
["cool"]
ghci> guard (1 > 2) >> return "cool" :: [String]
[]

Si guard réussit, le résultat qu’elle contient est un tuple vide. On utilise alors >> pour ignorer ce tuple vide et présenter quelque chose d’autre en retour. Cependant, si guard échoue, alors le return échouera aussi, parce que donner une liste vide à une fonction via >>= résulte toujours en une liste vide. guard dit simplement : si ce booléen est False, alors produis un échec immédiatement, sinon crée une valeur réussie factice avec (). Tout ce que cela permet est d’autoriser le calcul à continuer.

Voici l’exemple précédent réécrit en notation do :

sevensOnly :: [Int]
sevensOnly = do
    x <- [1..50]
    guard ('7' `elem` show x)
    return x

Si nous avions oublié de présenter x en résultat final avec return, la liste résultat serait seulement une liste de tuples vides. Voici la même chose sous forme de liste en compréhension :

ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]

La quête d’un cavalier

Voici un problème qui se prête particulièrement bien à une résolution non déterministe. Disons que vous ayez un échiquier, et seulement un cavalier placé dessus. On souhaite savoir si le cavalier peut atteindre une position donnée en trois mouvements. On utilisera simplement une paire de nombres pour représenter la position du cavalier sur l’échiquier. Le premier nombre détermine la colonne, et le second la ligne.

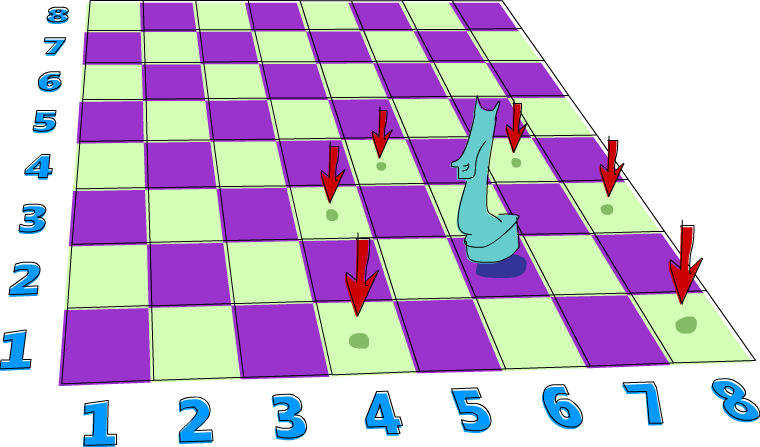
Créons un synonyme de type pour la position actuelle du cavalier sur l’échiquier :

type KnightPos = (Int,Int)

Donc, supposons que le cavalier démarre en (6, 2). Peut-il aller en (6, 1) en exactement trois mouvements ? Voyons. Si l’on commence en (6, 2), quel est le meilleur mouvement à faire ensuite ? Je sais, pourquoi pas tous les mouvements possibles ! On a à notre disposition le non déterminisme, donc plutôt que d’avoir à choisir un mouvement, choisissons-les tous à la fois. Voici une fonction qui prend la position d’un cavalier et retourne toutes ses prochaines positions :

moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = do
    (c',r') <- [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
               ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
               ]
    guard (c' `elem` [1..8] && r' `elem` [1..8])
    return (c',r')

Le cavalier peut toujours avancer d’une case horizontalement et de deux verticalement, ou bien de deux cases horizontalement et d’une verticalement. (c', r') prend chaque valeur de la liste des mouvements, puis guard s’assure que le déplacement obtenu (c', r'), reste bien dans les limites de l’échiquier. Si ce n’est pas le cas, elle produit une liste vide qui cause un échec, et return (c', r') n’est pas exécutée pour cette position là.

Cette fonction peut être réécrite sans utiliser les listes comme des monades, mais on l’a fait quand même pour l’entraînement. Voici la même fonction avec filter :

moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = filter onBoard
    [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
    ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
    ]
    where onBoard (c,r) = c `elem` [1..8] && r `elem` [1..8]

Les deux font la même chose, choisissez celle que vous trouvez plus jolie. Essayons :

ghci> moveKnight (6,2)
[(8,1),(8,3),(4,1),(4,3),(7,4),(5,4)]
ghci> moveKnight (8,1)
[(6,2),(7,3)]

Ça fonctionne à merveille ! On prend une position et on essaie tous les mouvements possibles à la fois, pour ainsi dire. À présent qu’on a une position non déterministe, on peut utiliser >>= pour la donner à moveKnight. Voici une fonction qui prend une position et retourne toutes les positions qu’on peut atteindre dans trois mouvements :

in3 :: KnightPos -> [KnightPos]
in3 start = do
    first <- moveKnight start
    second <- moveKnight first
    moveKnight second

Si vous lui passez (6, 2), la liste résultante est assez grande, parce que s’il y a beaucoup de façons d’atteindre une position en trois mouvements, alors le résultat est dans la liste de multiples fois. La même chose sans notation do :

in3 start = return start >>= moveKnight >>= moveKnight >>= moveKnight

Utiliser >>= une fois nous donne tous les mouvements possibles depuis le point de départ, puis en utilisant >>= une deuxième fois, pour chacun de ces premiers mouvements, les mouvements suivants sont calculés, et de même pour le dernier mouvement.

Placer une valeur dans un contexte par défaut en faisant return pour ensuite la passer à une fonction avec >>= est équivalent à appliquer la fonction normalement à la valeur, mais on le fait quand même pour le style.

À présent, écrivons une fonction qui prend deux positions et nous dit si on peut aller de l’une à l’autre en exactement trois étapes :

canReachIn3 :: KnightPos -> KnightPos -> Bool
canReachIn3 start end = end `elem` in3 start

On génère toutes les solutions possibles pour trois étapes, et on regarde si la position qu’on cherche est parmi celles-ci. Voyons donc si on peut aller de (6, 2) en (6, 1) en trois mouvements :

ghci> (6,2) `canReachIn3` (6,1)
True

Oui ! Qu’en est-il de (6, 2) et (7, 3) ?

ghci> (6,2) `canReachIn3` (7,3)
False

Non ! En tant qu’exercice, vous pouvez changer cette fonction afin que, lorsque vous pouvez atteindre une position depuis l’autre, elle vous dise quels mouvements faire. Plus tard, nous verrons comment modifier cette fonction pour qu’on puisse aussi lui passer le nombre de mouvements à faire plutôt que de le coder en dur comme ici.

Les lois des monades

Tout comme les foncteurs applicatifs, et les foncteurs avant eux, les monades viennent avec quelques lois que toutes les instances de Monad doivent respecter. Être simplement une instance de Monad ne fait pas automatiquement une monade, cela signifie simplement qu’on a créé une instance. Un type est réellement une monade si les lois des monades sont respectées. Ces lois nous permettent d’avoir des suppositions raisonnables sur le type et son comportement.

Haskell permet à n’importe quel type d’être une instance de n’importe quelle classe de types tant que les types correspondent. Il ne peut pas vérifier si les lois sont respectées, donc si l’on crée une nouvelle instance de la classe de types Monad, on doit être raisonnablement convaincu que ce type se comporte bien vis-à-vis des lois des monades. On peut faire confiance aux types de la bibliothèque standard pour satisfaire ces lois, mais plus tard, lorsque l’on écrira nos propres monades, il faudra vérifier manuellement que les lois tiennent. Mais ne vous inquiétez pas, elles ne sont pas compliquées.

Composition à gauche par return

La première loi dit que si l’on prend une valeur, qu’on la place dans un contexte par défaut via return et qu’on la donne à une fonction avec >>=, c’est la même chose que de donner directement la valeur à la fonction. Plus formellement :

• return x >>= f est égal à f x

Si vous regardez les valeurs monadiques comme des valeurs avec un contexte, et return comme prenant une valeur et la plaçant dans un contexte minimal qui présente toujours cette valeur, c’est logique, parce que si ce contexte est réellement minimal, alors donner la valeur monadique à la fonction ne devrait pas être différent de l’application de la fonction à la valeur normale, et c’est en effet le cas.

Pour la monade Maybe, return est définie comme Just. La monade Maybe se préoccupe des échecs possibles, et si l’on a une valeur qu’on met dans un tel contexte, c’est logique de la traiter comme un calcul réussi, puisque l’on connaît sa valeur. Voici return utilisé avec Maybe :

ghci> return 3 >>= (\x -> Just (x+100000))
Just 100003
ghci> (\x -> Just (x+100000)) 3
Just 100003

Pour la monade des listes, return place une valeur dans une liste singleton. L’implémentation de >>= prend chaque valeur de la liste et applique la fonction dessus, mais puisqu’il n’y a qu’une valeur dans une liste singleton, c’est la même chose que d’appliquer la fonction à la valeur :

ghci> return "WoM" >>= (\x -> [x,x,x])
["WoM","WoM","WoM"]
ghci> (\x -> [x,x,x]) "WoM"
["WoM","WoM","WoM"]

On a dit que pour IO, return retournait une action I/O qui n’avait pas d’effet de bord mais retournait la valeur en résultat. Il est logique que cette loi tienne ainsi pour IO également.

Composition à droite par return

La deuxième loi dit que si l’on a une valeur monadique et qu’on utilise >>= pour la donner à return, alors le résultat est la valeur monadique originale. Formellement :

• m >>= return est égal à m

Celle-ci peut être un peu moins évidente que la précédente, mais regardons pourquoi elle doit être respectée. Lorsqu’on donne une valeur monadique à une fonction avec >>=, cette fonction prend une valeur normale et retourne une valeur monadique. return est une telle fonction, si vous considérez son type. Comme on l’a dit, return place une valeur dans un contexte minimal qui présente cette valeur en résultat. Cela signifie, par exemple, pour Maybe, qu’elle n’introduit pas d’échec, et pour les listes, qu’elle n’ajoute pas de non déterminisme. Voici un essai sur quelques monades :

ghci> Just "move on up" >>= (\x -> return x)
Just "move on up"
ghci> [1,2,3,4] >>= (\x -> return x)
[1,2,3,4]
ghci> putStrLn "Wah!" >>= (\x -> return x)
Wah!

Si l’on regarde de plus près l’exemple des listes, l’implémentation de >>= est :

xs >>= f = concat (map f xs)

Donc, quand on donne [1, 2, 3, 4] à return, d’abord return est mappée sur [1, 2, 3, 4], résultant en [[1],[2],[3],[4]] et ensuite ceci est concaténé et retourne notre liste originale.

Les lois de composition à gauche et à droite par return décrivent simplement comment return doit se comporter. C’est une fonction importante pour faire des valeurs monadiques à partir de valeurs normales, et ce ne serait pas bon que les valeurs qu’elle produit fassent des tas d’autres choses.

Associativité

La dernière loi des monades dit que quand on a une chaîne d’application de fonctions monadiques avec >>=, l’ordre d’imbrication ne doit pas importer. Formellement énoncé :

• (m >>= f) >>= g est egal à m >>= (\x -> f x >>= g)

Hmmm, que se passe-t-il donc là ? On a une valeur monadique m, et deux fonctions monadiques f et g. Quand on fait (m >>= f) >>= g, on donne m à f, ce qui résulte en une valeur monadique. On donne ensuite cette valeur monadique à g. Dans l’expression m >>= (\x -> f x >>= g), on prend une valeur monadique et on la donne à une fonction qui donne le résultat de f x à g. Il n’est pas facile de voir que les deux sont égales, regardons donc un exemple qui rend cette égalité un peu plus claire.

Vous souvenez-vous de notre funambule Pierre qui marchait sur une corde tendue pendant que des oiseaux atterrissaient sur sa perche ? Pour simuler les oiseaux atterrissant sur sa perche, on avait chaîné plusieurs fonctions qui pouvaient mener à l’échec :

ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)

On commençait avec Just (0, 0) et on liait cette valeur à la prochaine fonction monadique, landRight 2. Le résultat était une nouvelle valeur monadique qui était liée dans la prochaine fonction monadique, et ainsi de suite. Si nous parenthésions explicitement ceci, cela serait :

ghci> ((return (0,0) >>= landRight 2) >>= landLeft 2) >>= landRight 2
Just (2,4)

Mais on peut aussi écrire la routine ainsi :

return (0,0) >>= (\x ->
landRight 2 x >>= (\y ->
landLeft 2 y >>= (\z ->
landRight 2 z)))

return (0, 0) est identique à Just (0, 0) et quand on le donne à la lambda, x devient (0, 0). landRight prend un nombre d’oiseaux et une perche (une paire de nombres) et c’est ce qu’elle reçoit. Cela résulte en Just (0, 2) et quand on donne ceci à la prochaine lambda, y est égal à (0, 2). Cela continue jusqu’à ce que le dernier oiseau se pose, produisant Just (2, 4), qui est effectivement le résultat de l’expression entière.

Ainsi, il n’importe pas de savoir comment vous imbriquez les appels de fonctions monadiques, ce qui importe c’est leur sens. Voici une autre façon de regarder cette loi : considérez la composition de deux fonctions, f et g. Composer deux fonctions se fait ainsi :

(.) :: (b -> c) -> (a -> b) -> (a -> c)
f . g = (\x -> f (g x))

Si le type de g est a -> b et le type de f est b -> c, on peut les arranger en une nouvelle fonction ayant pour type a -> c, de façon à ce que le paramètre soit passé entre les deux fonctions. Et si ces deux fonctions étaient monadiques, et retournait des valeurs monadiques ? Si l’on avait une fonction de type a -> m b, on ne pourrait pas simplement passer son résultat à une fonction de type b -> m c, parce que la fonction attend un b normal, pas un monadique. On pourrait cependant utiliser >>= pour réaliser cela. Ainsi, en utilisant >>=, on peut composer deux fonctions monadiques :

(<=<) :: (Monad m) => (b -> m c) -> (a -> m b) -> (a -> m c)
f <=< g = (\x -> g x >>= f)

On peut à présent composer deux fonctions monadiques :

ghci> let f x = [x,-x]
ghci> let g x = [x*3,x*2]
ghci> let h = f <=< g
ghci> h 3
[9,-9,6,-6]

Cool. Qu’est-ce que cela a à voir avec la loi d’associativité ? Eh bien, quand on regarde la loi comme une loi de composition, elle dit que f <=< (g <=< h) doit être égal à (f <=< g) <=< h. C’est juste une autre façon de dire que l’imbrication des opérations n’importe pas pour les monades.

Si l’on traduit les deux premières lois avec <=<, la composition de return à gauche dit que pour toute fonction monadique f, f <=< return est égal à f et celle à droite dit que return <=< f est aussi égal à f.

Dans ce chapitre, on a vu quelques bases des monades et appris comment la monade Maybe et la monade des listes fonctionnent. Dans le prochain chapitre, nous regarderons tout un tas d’autre monades cool, et on apprendra à créer les nôtres.